by Sergiu Baluta, Starlino Electronics, revised 10/30/2015
This article is a theoretical venture that aims to answer a series of practical questions, such as:
– given a certain electrical setup that can generate a certain power, what is the maximum thrust that we can achieve ?
– can a human-powered aircraft be built ?
– can I tell the expected thrust generated by a copter simply by knowing the power it consumes and vice-versa ?
– are larger propellers really more “efficient” ?
– which multicopter configuration is more efficient: tricopter , quadcopter , hexacopter or octacopter ?
– I heard that for every gram of mass I add to my multicopter, the flight time will decrease by 1 second, can you put any sense in this ?
– and many more…
When selecting motors for an RC model you will often come across the thrust tables that tell you how much thrust (or “pull”) a specific motor can generate. This usually depends on few factors: the propeller used and the voltage applied. Next to these two parameters you will usually see the current and power consumed and the resulting thrust generated, usually expressed in grams. If you want your model to hover, you must ensure that your motors can generate a thrust equal to or greater than the mass of the model.
The power that your motor consumes is calculated based on the simple formula:
P = V * I , where V is the voltage and I is the current.
Power represents the amount of energy we’re consuming per second, which is expressed as follows:
P = E / t, where E is the energy.
The efficiency of a specific setup consisting of a propeller and a motor is often calculated as:
Eff = Thr / P , where Thr is the thrust force generated expressed in grams and P is the power consumed expressed in Watts.
However this efficiency is not expressed in percentage as you would usually expect so it does not tell us if our motor-propeller setup is consuming energy exclusively to generate lift or wasting it somewhere else. To compute an efficiency value in percentage we would need to know the minimum or “ideal” power necessary to generate a specific thrust given our setup and environment.
We have to mention from the start that such an “ideal” model, taking into account all the possible factors would probably be too complex to use for practical purposes. So instead our goal is to first deduct and then define a “theoretical” or “reference” power formula. Finally this formula will be applied to a series of practical experiments and the resulting “theoretical” power will be compared to the real-world observed power. To avoid confusion with the other efficiency let’s call this ratio “Theoretical Thrust Ratio” or TTR:
TTR = P(real) / P(theoretical)
So let’s dive into our calculations. But before we do that, for the impatient reader, here are the formulas that we’ll be deducting and using for computing our “theoretical” power (or thrust – if we flip the formula around):
Here P is the power expressed in Watts., F is the thrust expressed in Newtons, r is the radius of the propeller expressed in meters and K is a air density dependent coefficient, with a nominal value of 0.3636 assuming air pressure of 1atm and air temperature of 20C.
The formulas above are expressed in international physical units, however for those doing RC I am also providing the following convenient formula for computing thrust in grams Tgram, based on a propeller diameter expressed in inches Dinch:
Here C is an air density dependent coefficient with a nominal value of 0.0278 assuming air pressure of 1atm and air temperature of 20C.
Below is a lookup table for K and C coefficients at various temperatures and air pressure of 1atm.
| Temperature (degrees C) |
Air Density (kg/m^3) @ 1atm | K | C |
| 35 | 1.1455 | 0.372745594 | 0.02850295 |
| 30 | 1.1644 | 0.369708101 | 0.02827068 |
| 25 | 1.1839 | 0.366650731 | 0.028036891 |
| 20 | 1.2041 | 0.363562254 | 0.027800722 |
| 15 | 1.225 | 0.360447503 | 0.027562545 |
| 10 | 1.2466 | 0.357311097 | 0.027322712 |
| 5 | 1.269 | 0.354143483 | 0.027080492 |
| 0 | 1.2922 | 0.35094996 | 0.026836291 |
| −5 | 1.3163 | 0.347722365 | 0.026589484 |
| −10 | 1.3413 | 0.344466588 | 0.026340523 |
| −15 | 1.3673 | 0.341175753 | 0.026088881 |
| −20 | 1.3943 | 0.337856246 | 0.025835046 |
| −25 | 1.4224 | 0.334502366 | 0.025578583 |
The Deduction
Let’s get back to the main question of this article – “how much power is needed to hover an object ?” , or in other words how much energy we need to consume per second to maintain this object “in the air”. Well, as it turns out “it all depends…”. For example we do not need to consume any energy to keep a book on a shelf or a tire suspended on a rope. Clearly we did not formulated our question correctly! So let’s try again and this time be more specific. “How much power does a craft powered by a spinning propeller needs in order to hover in the air ?” Here you go – much better ! Let’s see if we can answer this question.
You might recall from school physics a rule called “preservation of energy”, it simply states that the energy does not like to go away or disappear, all it does – it transforms from one form to another. We certainly know that our craft consumes energy in the form of electricity or burned fuel, but where does it go ? Didn’t we say that we don’t need energy to hover an object such as a book on a shelf or a tire hanging on a rope ? The reality is that not every object is as lucky as a book on a shelf or a tire suspended on a rope. In both these cases – the book and the tire have the benefit of a “reaction force” of the shelf and rope respectively. The book pushes on the shelf with its weight and the shelf will always push back with an equal force in the opposite direction. If you’re confused it’s probably because of a common misconception that an existence of a “force” implies that energy is consumed. The later is not true – a “force” can exist simply because of the setup of the nature, for example the gravitational force, the magnetic force and the reactive force they all simply exists without consuming energy. It’s their action that might or might not lead to the transfer of energy.
Back to our model of a propeller-powered craft, since our craft is suspended in the air, there must clearly exist an opposing force F that is directed in a opposite direction:
F = m * g , where m is the mass of our craft and g is the acceleration of gravity ( approximately 9.8 m / s^2 ).
In fact this force is not much different from the “reaction force” that a shelf exerts on the book, except our medium “the air” is less dense than the shelf and as a result of this force, as we push “against” it with the propeller, the air starts moving. Here you go! We found were our energy goes. The electrical or fuel energy consumed by an aircraft is transferred to the kinetic energy of the moving air.
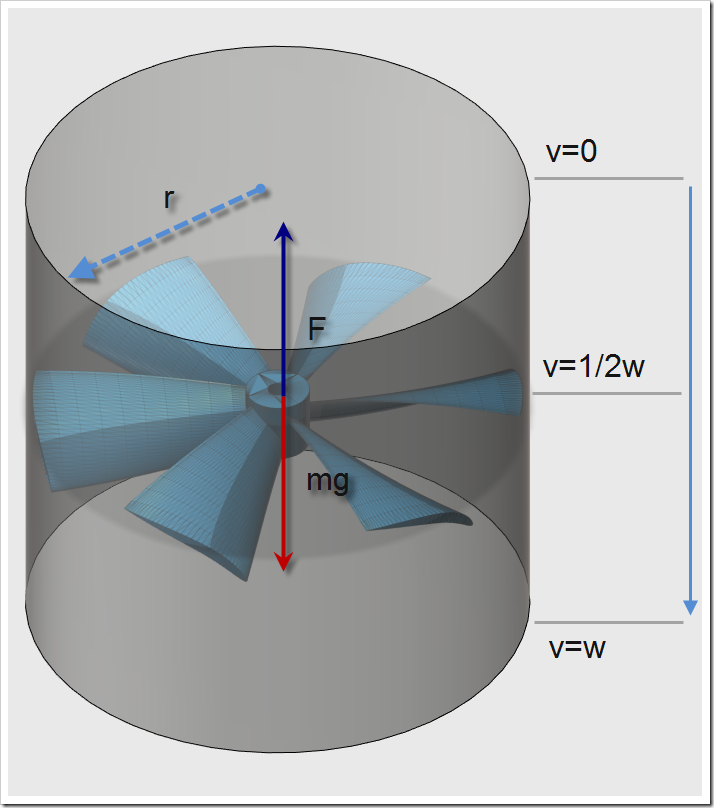
Let’s imagine a spinning rotor that generates a thrust F (in case of hover it is equal to mg) and a cylinder of air of infinite height with the rotor placed in the middle. The rotor is sucking air from the top and then pushing it down from the bottom. The rotor will have very little influence on the air on the top (since it’s very-very far away) so we can assume the speed of the air starts at 0, then slowly increases as it passes the rotor to w/2 (due to symmetry of our model from top and bottom) and finally as it reaches the bottom of the cylinder it stabilizes at a speed w, again rotor has very small influence on the air from the bottom of cylinder since it’s far-far away.
Let’s examine our model for a period of time t that it takes for a particle of air to travel from the top to bottom of cylinder . Let’s note the area of the cross-section of our cylinder as A and since it’s defined by the radius of our rotor we have:
![]()
The volume of air Vol that passes through the rotor during the time t, can be calculated by monitoring how much “height” of air passes through the rotor at the speed v, h=v*t and multiplying by the cross section area A.
![]()
Given the air density Qair we can calculate the mass of air that passes through the rotor in the time period t:
![]()
Let’s note that since the air starts at zero speed so its starting momentum is zero, thus it’s momentum change will be equal to final momentum Mair * w, where w is the final speed. From momentum conservation theory we can recall that the force that we apply on a mass is equal to the rate of change of momentum:
![clip_image002[19] clip_image002[19]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00219.gif)
Finally combining the last two formulas we get:
![clip_image002[21] clip_image002[21]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00221.gif)
From here we can get the speed v at the rotor:
![clip_image002[23] clip_image002[23]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00223.gif)
Next let’s note that the power is equal to the rate at which work is done or in other words rate at which energy is consumed. Work is given by the formula W=F*d (where d is the distance), thus power is P = W /t = F*d/t = F*v:
Note that we substituted the circle area A = PI*r^2 formula. Finally, by extracting some coefficients we get:
![clip_image002[35] clip_image002[35]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00235.gif)
and the inverse formula for thrust is:
![clip_image002[51] clip_image002[51]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00251.gif)
The formulas above work with international physics units, thrust F is measured in Newtons, and radius r is measured in meters. For practical purposes in RC we work with propeller diameter in inches and thrust is calculated in grams (which is equivalent to mass this thrust force can hover from F = mg formula, where g is standard gravity ~ 9.8m/s^2). So let’s define another equivalent set of formulas:
![clip_image002[45] clip_image002[45]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00245.gif)
![clip_image002[3] clip_image002[3]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00232.gif)
![clip_image002[5] clip_image002[5]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00252.gif)
and the inverse formula is
![clip_image002[53] clip_image002[53]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00253.gif)
Experimental Results
To verify these theoretical results I conducted a series of thrust tests using different motors and propellers commonly used in RC. Also I verified thrust tables randomly found on the internet (forums or motor specs):
Motor: DYS 1306 3100KV BX Source: http://www.banggood.com/DYS-1306-3100KV-BX-Series-Brushless-Motor-For-Multicopter-CW-CCW-p-962149.html
| Prop Diam " | Prop Ptich | V | A | Thrust(g) | W | Eff (g/W) | Theoretical Thrust (g) | TTR=Thrust /Theoretical Thrust |
| 5 | 3 | 7.4 | 1.4 | 70 | 10.36 | 6.8 | 151 | 46.2% |
| 5 | 3 | 7.4 | 3.3 | 140 | 24.42 | 5.7 | 268 | 52.2% |
| 5 | 3 | 7.4 | 5.7 | 220 | 42.18 | 5.2 | 386 | 57.0% |
| 5 | 3 | 11.1 | 2.1 | 100 | 23.31 | 4.3 | 260 | 38.5% |
| 5 | 3 | 11.1 | 5.5 | 210 | 61.05 | 3.4 | 494 | 42.5% |
| 5 | 3 | 11.1 | 9.4 | 350 | 104.34 | 3.4 | 706 | 49.6% |
| 6 | 2 | 7.4 | 1.3 | 70 | 9.62 | 7.3 | 163 | 43.0% |
| 6 | 2 | 7.4 | 3.7 | 150 | 27.38 | 5.5 | 327 | 45.9% |
| 6 | 2 | 7.4 | 7.9 | 230 | 58.46 | 3.9 | 542 | 42.4% |
Motor: EMAX MT1804 2480KV Source: http://www.rcgroups.com/forums/showthread.php?t=2172324
| Prop Diam " | Prop Ptich | V | A | Thrust(g) | W | Eff (g/W) | Theoretical Thrust (g) | TTR=Thrust /Theoretical Thrust |
| 5 | 3 | 12.1 | 7.3 | 345 | 88.33 | 3.9 | 632 | 54.6% |
| 5 | 3 | 12.2 | 6.2 | 330 | 75.64 | 4.4 | 570 | 57.9% |
| 5 | 4 | 12.1 | 9 | 370 | 108.9 | 3.4 | 727 | 50.9% |
| 6 | 3 | 12.2 | 8.6 | 410 | 104.92 | 3.9 | 800 | 51.2% |
Motor: DYS BE1806 2300KV Source: http://www.rcgroups.com/forums/showthread.php?t=2180080That
| Prop Diam " | Prop Ptich | V | A | Thrust(g) | W | Eff (g/W) | Theoretical Thrust (g) | TTR=Thrust /Theoretical Thrust |
| 5 | 3 | 12 | 9 | 415 | 108 | 3.8 | 723 | 57.4% |
| 5 | 3 | 12.2 | 3.6 | 230 | 43.92 | 5.2 | 397 | 58.0% |
| 5 | 3 | 12.1 | 7.5 | 360 | 90.75 | 4.0 | 643 | 55.9% |
| 5 | 3 | 12.2 | 3.3 | 205 | 40.26 | 5.1 | 374 | 54.8% |
| 5 | 4 | 12 | 10.6 | 440 | 127.2 | 3.5 | 806 | 54.6% |
| 5 | 4 | 12.1 | 4.2 | 225 | 50.82 | 4.4 | 437 | 51.5% |
| 6 | 3 | 12 | 10.2 | 485 | 122.4 | 4.0 | 887 | 54.7% |
| 6 | 3 | 12.1 | 4 | 240 | 48.4 | 5.0 | 478 | 50.2% |
| 6 | 4.5 | 11.8 | 16.1 | 580 | 189.98 | 3.1 | 1189 | 48.8% |
| 6 | 4.5 | 12 | 5.1 | 235 | 61.2 | 3.8 | 559 | 42.1% |
| 5 | 3 | 16.3 | 11.5 | 570 | 187.45 | 3.0 | 1044 | 54.6% |
| 5 | 3 | 16.4 | 5.1 | 280 | 83.64 | 3.3 | 609 | 45.9% |
A more extensive list of test can be downloaded here, the Excel Spreadsheet contains a _TEMPLATE_ sheet that you can use to fill in and verify your own data:
http://starlino.com/wp-content/uploads/data/power_thrust/Motor_Thrust_Tests.xlsx
Example Uses
Q: Can I build a human powered helicopter ?
A: A trained cyclist can generate 500W peak power (or even 1500W according to some reports), let’s a assume the cyclist weights 70Kg and the weight of the copter is 30Kg, thus the thrust needed for lift off is 100Kg. From this formula:
![clip_image002[55] clip_image002[55]](http://www.starlino.com/wp-content/uploads/2017/09/clip_image00255.gif)
we can compute the radius of the propeller that this human-powered helicopter will need to have :
r = K * (mg) ^ (3/2) / P = 0.3636 * (100*9.8) ^ (3/2) / 500 = 22.3 (meters)
In fact human powered machines have been built. Let’s analyze for example the Gamera II built by University of Maryland:
Weight: ~ 37kg + Pilot ~ 90kg
Rotors Radius: ~ 7.2m ( x 4)Since this craft has 4 rotors , each rotor would need to produce at least 1/4 of the thrust or 90Kg / 4 = 22.5Kg . Using our formula we can calculate power needed for each rotor:
P = K * (mg) ^ (3/2) / r = 0.3636 * (22.5*9.8) ^ (3/2) / 7.2 = 165.35
Thus the total power required is estimated at 165.35W*4 = 661.4 W , which is quite manageable for a trained cyclist. In reality no motor is 100% efficient. Still, an advantageous effect for take-off is the “ground effect”. As air is pushed into the ground its density increases, as a result our K coefficient will decrease, meaning there’s less power required to generate same thrust compared to less dense air.
Q: I am buying a motor that is rated at 200W, assuming I will use a battery that has a voltage high enough to result in all 200W being drawn from the motor and a 10” prop, how much thrust can I expect from this motor and what will be the gram/Watt efficiency ?
A: Simply apply this formula to get the thrust in grams:
Tgrams = ( P * Dinch / C) ^ (2/3) = ( 200 * 10 / 0.0278) ^ (2/3) =~ 1730 gram, gram/Watt efficiency immediately follows: Eff = 1730 / 200 = 8.65. From practice, knowing that most brushless motors setup used in RC will deliver 50-60% of theoretical thrust and efficiency you can divide the above theoretical values by 2 to get a real-life estimate , so P ~ 865g, Eff ~ 4.3 g/ W.
revised 10/30/2015
by Sergiu Baluta, Starlino Electronics

![clip_image002[55] clip_image002[55]](http://www.starlino.com/wp-content/uploads/2017/09/clip_image00255_thumb.gif)
![clip_image002[57] clip_image002[57]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00257_thumb.gif)
![clip_image002[59] clip_image002[59]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00259_thumb.gif)
![clip_image002[61] clip_image002[61]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00261_thumb.gif)
![clip_image002[67] clip_image002[67]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00267_thumb.gif)
![clip_image002[65] clip_image002[65]](http://www.starlino.com/wp-content/uploads/2015/10/clip_image00265_thumb.gif)
![clip_image002[5] clip_image002[5]](http://www.starlino.com/wp-content/uploads/2017/09/clip_image0025_thumb.gif)
Please note that on 10/30/2015 I revised completely this article and calculations. Thanks to Olli and others who pointed out ways to improve it, your input is much appreciated ! In order not to confuse future readers I removed the comments that where related to old article. Thank you !
Thank you very much for very clear explanations and broad set of data. There may be some logical extension to your analysis. You include prop pitch values, but its effect on overall picture is only in actual motor power consumption, so it is not needed for your analysis. But it is very important for copter agility and the health of its elecrtic system. If you use 2212 2600kv motor with 6" prop with 4.5" pitch it will generate about 700 to 900 g thrust, but even 30A ESC will be very hot and there is a potential to catch fire (I have seen how ESC burst in flames). The use of 3" pitch prop will reduce consumed power almost two times. So, there are high RPM motors with high kv-rating (but it is not ultimate parameter, the hight of rear earth magnets also plays big role), and slow, high torgue motors. It would be good to have the extension of your paper towards incorporation of prop pitch, motor kv rating and ESC amperage. Not in formal form of classical physics, but rather in the form of an estimation or approximate formula. I would be happy to help as much as I can. I have very vague undersanding of ESC principle, but their amperage rating seems to be not very trustful, and what is the amperage of 3-phase variable frequency current? Sorry for lengthy comment. I appreciate any input on raised questions.
Thank you so much!
If only expensive textbooks were half as good as you!
Or maybe I’m the problem, as my name suggests
“(work and power are both defined by the rate of change of energy)”
This is incorrect. Work is the time integral of power or vie versa power is the rate of change of work. Say you push a block on a surface. Work is how much energy to push from A to B. Power is the rate at w.ich you did it.
Thanks for catching that. I amended that paragraph.
Isn’t the short answer 9.8N/kg?
Oops, 9.8Nm/s/kg I should have said.
Ken, and this would be based on what formula ?
This makes no sense – what is stopping me from using huge propeller to achieve more thrust? Formula lacks something. Probably torque.
The formula simply describes the relationship between F / P given you were able to transfer that power to the air. It does not state that given a propeller large enough you can transfer infinite power to the air with same ~50% efficiency. For example if your propeller has zero pitch it will just cut through air and not generate any thrust but also not pull any power. It also happens the larger the prop, the lower the pitch must be. The farther away from the center of prop the lower the pitch on the prop needs to be to balance the load on prop so it does not bend.
So you should use this formula understanding its limitation. It can be useful as general rule of thumb for calculating the amps of your ESC or flight time given mAH of your batteries, assuming the designers of your RC gear have done a good job and you can target that 50% efficiency. Of course in real life your millage will vary.
Ah, no movement means no power is consumed. I am starting to see why the “question” is not formed well and has a complicated answer.
hello i liked your post too much
i want to design a quad copter that can lift 600kg can tell all about
Great,
looks your math gives the same result for thrust I found here:
http://www.dept.aoe.vt.edu/~lutze/AOE3104/thrustmodels.pdf
Here are more examples of flight time and efficiency for different types of copters (gasoline, electric, man powered)
https://mshtools.wordpress.com/2017/07/13/lkjkjkj/
and what if you divide by two theoretical trust it will be more presailsly
Shouldn’t v be equal to sqrt[2F/(rhoXA)]
I’m a little confused. Suppose we flip this problem on its head, and try to maximize the Thrust/Power ratio.
The formula F = (Pr/K)^(2/3) seems to suggest that if we just let the propeller radius (r) go to infinity, we will be able to generate infinite thrust using only a finite amount of power – which seems wrong.
I think the relation b/w F, P and r can’t be monotonic.
What would be the best way to answer the question: What motor+propeller combo should I use to maximize efficiency for a given thrust?
power = force × velocity